Yesterday I linked to an IBM site which puts up a new, pretty cool math problem every month. The one for this month is simplicity itself, “what is the size of the largest square that will fit in the unit cube?” I sent this to my math homies at work because day-job is great, but every once in a while you need a good shot in the brain. Chuck, who I am now calling “Patty O’Spoilerton”, immediately recognized the problem as something he had seen as a young nerdling at school and emailed us all a website with the “solution“.
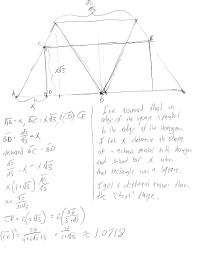
Thing is, that site really glosses over some very important details. It sets us on the right track of viewing the cube from above a vertex so it resembles a hexagon, but then they just toss out some number for the largest square to fit in a hexagon. That became our problem… given a hexagon, what is the largest square that will fit inside? Here’s my answer.
Wouldn’t it be cool to make two cubes with the proper holes cut into each? You could pass cube A through cube B then cube B through A in an endless juggling T.A.R.D.I.S-style mindfuck loop. Put this down on the list of ways to blow your future grandkid’s minds.
Update: Paul found the answer on the Wolfram site, and I was wondering why it differed from mine even though they seemed like the same square. The solution we were solving is not what the problem was really asking. The area of the largest hole that can be cut in a cube is not the largest square that can fit inside a cube. The former is smaller than the latter. Sure, they may look the same from a certain perspective (right above the vertex), but the area of the square is a nice 1.125, not some irrational number.
Hey Brian,
That answer is wrong. I mean, I think it is the answer they are looking for but it is not the answer to the question they asked. That is the answer to Prince Rupert’s cube problem, but they did not ask what is the face size of the largest cube that can pass through a unit cube. That is the square cross section of the hole that can be cut into the unit cube to allow the larger cube to be passed through it.
The square with vertices (0,0,0), (1,0,1/2),(1,1,1), and (0,1,.5) fits entirely with the unit cube and has an area of 1.25. It actually divides the cube into two equal pieces.
I’ve emailed the Wolfram site to let them know they have a mistatement on the page you linked to, however they do have a good explanation of Prince Rupert’s problem there. There is a link to it at the bottom of the page you linked to.
Hey,
Forget my comments, I must have been smoking something to think that was a square. The quadrilateral points are coplanar, but not a square.
Kevin.